Die Ausrichtung der Sonnenuhr
Aus Symmetriegründen richten wir die Projektionsebene (in der Folge nennen wir diese Zifferblatt) so aus, dass diese im Frühjahrspunkt (21. März) und im Herbstpunkt (23. September) um 12 Uhr Sonnenzeit (SZ) senkrecht zur Strahlrichtung steht. Dies ist dann erfüllt, wenn das Zifferblatt gegenüber einer horizontalen Ebene einen Winkel von 46,926o einschliesst (die Sonnenuhr befindet sich auf dem 46.926o–Breitenkreis) und die Sonnenuhr gegen Süden ausgerichtet ist (s. Fig. 1).

Anordnung der Löcher für 9 Uhr SZ bis 15 Uhr SZ
Wir gehen vom Loch 12 Uhr SZ (SZ=Sonnenzeit) aus und möchten auf dem Zifferblatt eine 15-Minuten-Skala. In 15 Minuten überstreicht die Sonne einen Winkel von 3.75o. Damit ist die Skala festgelegt (s. Fig. 2). Es stellt sich nun die Frage, wie wir die übrigen Löcher anordnen müssen, damit wir dieselbe Skala für die übrigen Löcher nutzen können. Hierzu müssen die Löcher einerseits auf Geraden liegen, die zur Senkrechten im Punkt M00 (s. Fig. 2) einen Winkel von n * 15o ( n = +/- 1, +/- 2, +/- 3) einschliessen. Andererseits sollten bei jedem Loch die Strahlen, die durch die Punkte M-30 und M+30 gehen einen Winkel von 15o (60 Minuten Sonnenbewegung) und die Strahlen, die durch die Punkte M-15 und M+15 gehen einen Winkel von 7.5o (30 Minuten Sonnenbewegung) einschliessen.
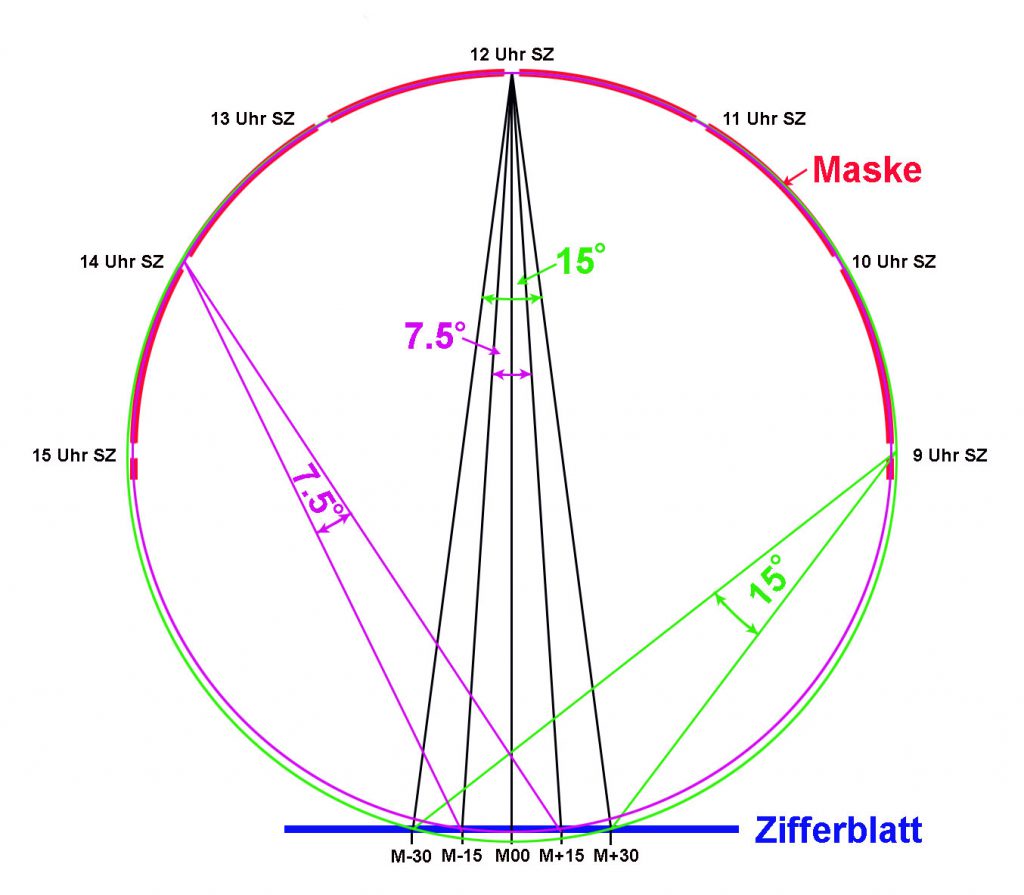
Diese zweite Bedingung entspricht dem geometrischen Ortsbogen (manchmal auch Fasskreisbogen genannt): «Der Ortsbogen ist der Ort aller Punkte, von denen aus man eine Sehne unter gleichem Winkel sieht.» Der Kreis, der durch das Loch 12 Uhr SZ und die Punkte M-30 und M+30 bestimmt wird, bildet den Ortsbogen für 15o (in Fig. 2 grün dargestellt) und der Kreis durch das Loch 12 Uhr SZ und die Punkte M-15 und M+15 gebildet wird (in Fig. 2 violett dargestellt) bildet den Ortsbogen für 7.5o. Die beiden Ortsbogen sind nicht identisch, was bedeutet, dass eine mathematisch exakte Lösung nicht existiert. Bei der realen Sonnenuhr wählen wir für die Maske einen Halbkreis mit dem Radius R und positionieren diesen um den Betrag R oberhalb des Zifferblattes [das Zifferblatt als Tangente an den Kreis mit Radius R = Grenzwert für immer kleinere Winkel]
Fig. 2 zeigt uns, dass die gewählte Geometrie der Maske eine gute Näherung an die gewünschten Eigenschaften bildet. Bei der Berechnung des Zifferblattes wird die reale Geometrie eingesetzt, sodass die berechneten Skalen die «Unexaktheiten» unserer Näherung enthalten. Da die Abweichungen der Ortsbogen vom gewählten Masken-Kreis bei 9 Uhr SZ und bei 15 Uhr SZ am grössten ist, müssen wir erwarten, dass bei diesen Zeiten die Abweichungen von der 12 Uhr SZ – Skala am grössten sind. Die Mitberücksichtigung der Zeitgleichung führt dazu, dass die Abweichungen asymmetrisch sind.

